실수를 저장할 때 고정소수점 방식과 부동소수점 방식이 있다.
고정소수점
- 정수를 표현하는 비트 수와 소수를 표현하는 비트 수를 미리 정해놓고, 해당 비트만큼만 사용해서 숫자를 표현하는 방식이다.
- 정수를 표현하는 bit를 늘리면 큰 숫자를 표현할 수 있지만 정밀한 숫자를 표현하기에는 힘들다. 그래서 소수를 표현하는 bit를 늘릴 경우 정밀한 숫자를 표현할 수 있지만 큰 숫자를 표현하지 못한다.
- 이러한 문제를 해결하기 위해 부동소수점을 사용하고 있다.
부동소수점
- 소수점의 위치를 고정하지 않고, 그 위치를 나타내는 수를 따로 적는 방식이다. (가수)×(밑수)(지수)
- 일반적으로 IEEE 754 방식을 사용하고 있다.
IEEE 754
IEEE 754는 전기전자기술자협회(IEEE)에서 개발한 표준 부동소수점 방식이며, 현재 컴퓨터에서 가장 널리 쓰이는 방식이다.
- 실수 표기 방식, 실수 연산에 대한 규정, 오버플로우/언더플로우 처리, 반올림에 대한 규정 등을 포함한다.
구조
필수요소

- 부호 부분(Sign)
- 지수 부분(Exponent)
- 가수 부분(Mantissa, Fraction)
표현방법
- 부호 부분은 양수일 경우 0, 음수일 경우 1로 표현한다.
- 절댓값을 이진법으로 나타낸다.
- 소수점을 왼쪽으로 이동시켜, 왼쪽에는 1만 남게 만든다.
- 가수 부분은 소수점의 오른쪽 부분이다. 부족한 비트 수만큼 0으로 채운다.
- 지수 부분은 지수승에 Bias를 더한다.
규격
- 32비트 단정밀도(single-precision)
- 부호 1비트, 지수부 8비트, 가수부 23비트
- 64비트 배정밀도(double-precision)
- 부호 1비트, 지수부 11비트, 가수부 52비트
- 43비트 이상의 확장 단정밀도(거의 쓰이지 않음)
- 79비트 이상의 확장 배정밀도(일반적으로 80비트로 구현됨)
이 중 32 비트 단정밀도는 반드시 구현해야 하며, 다른 형식은 선택사항이다. 많은 프로그래밍 언어에서 IEEE 표준을 따르도록 정의하고 있다. (C에서는 float는 단정밀도, double은 배정밀도와 대응된다.)
범위
값은 아래 x와 같다.

- 항상 소수점 왼쪽에 1을 남기기 때문에 fraction 비트로 표현하지 않아도 된다.
- exponent는 항상 unsigned 되도록 하기위해 Bias를 추가해서 비트에 표현한다. single bias = 127, double bias = 1023
| 형식 | 지수 길이 | 가수 길이 |
|---|---|---|
| float | 8비트 | 23비트 |
| double | 11비트 | 52비트 |
float은 32비트 단일 정확도이며, double은 64비트 이중 정확도 숫자이다.
최소값
float(32bit)의 최소값은
- Exponent = 00000001
- 실제 지수 값(Exponent - Bias) : 1 - 127 = -126
- Fraction = 000…00
- 실제 가수 값(1.0 + Fraction) = 1.0 + 0
- 최소값 = ± 1.0 * 2 -126 , 약 1.2 * 10-38
double(64bit)의 최소값은
- Exponent = 00000001
- 실제 지수 값(Exponent - Bias) : 1 - 1023 = -1022
- Fraction = 000…00
- 실제 가수 값(1.0 + Fraction) = 1.0 + 0
- 최소값 = ± 1.0 * 2 -1022 , 약 2.2 * 10-308
최대값
float(32bit)의 최대값은
- Exponent = 11111110
- 실제 지수 값(Exponent - Bias) : 254 - 127 = 127
- Fraction = 1111…11
- 실제 가수 값(1.0 + Fraction) = 1.0 + 1
- 최소값 = ± 2.0 * 2 127 , 약 3.4 * 1038
double(64bit)의 최대값은
- Exponent = 111…110
- 실제 지수 값(Exponent - Bias) : 2046 - 1023 = 1023
- Fraction = 1111…11
- 실제 가수 값(1.0 + Fraction) = 1.0 + 1
- 최소값 = ± 2.0 * 2 1023 , 약 1.8 * 10308
정리하자면 아래와 같다.
| 형식 | 최소값 | 최대값 |
|---|---|---|
| float | 1.175494351 E - 38 | 3.402823466 E + 38 |
| double | 2.2250738585072014 E - 308 | 1.7976931348623158 E + 308 |
정확도
가수부 비트 수에 따라서 달라진다.
- float(32bit) : 2진수 23자리, 10진수 약 6-7자리
- double(64bit) : 2진수 52자리, 10진수 약 16-17자리
무한대, 숫자가 아닌 값
부동 소수점 숫자에는 특별한 두 가지 숫자가 있다.
무한대(infinity, inf)
부동소수점에서 0으로 나누면 오버플로우가 발생하지 않고 ±∞를 나타내야 한다.
1.0 / 0.0은 양의 무한대가 되고, 1.0 / -0.0은 음의 무한대가 된다.
숫자가 아닌 값 (Not a Number, NaN)
NaN은 순서가 정해져있지 않기 때문에 <, ㅡ=, >, >= 연산을 수행할 경우 항상 그 결과는 false가 된다.
부동소수점 정밀도 오류
부동소수점 숫자가 까다로운 이유 중 하나는 2진법과 10진법 간의 차이가 크기 때문이다. 1/10은 10진법에서는 0.1로 표현되지만, 2진법에서는 0.00011001100110011… 과 같은 무한 시퀀스로 표현된다. 이 때문에 부동소수점 숫자에 0.1을 지정하면 정밀도 문제가 발생한다.
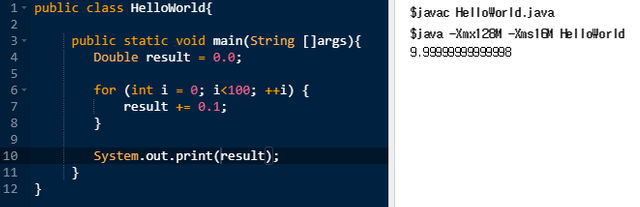
이와 같이 오류가 발생하여 Java에서는 돈 계산과 같이 정확한 계산이 요구될 때는 java.math.BigDecimal이라는 클래스를 사용해야만 한다.
숫자를 부동소수점으로 변환하는 사이트
https://www.h-schmidt.net/FloatConverter/IEEE754.html
출처 📎
- wikipedia - IEEE 754
- wikipedia - 부동소수점
- https://steemit.com/kr/@modolee/floating-point
- https://velog.io/@sangmin7648/%EC%98%A4%EB%8A%98%EC%9D%98-%EB%B0%B0%EC%9B%80-014-%EC%BB%B4%ED%93%A8%ED%84%B0%EA%B5%AC%EC%A1%B0-%EB%B6%80%EB%8F%99%EC%86%8C%EC%88%98%EC%A0%90 - 최소최대값, 덧셈방식
- https://learn.microsoft.com/ko-kr/cpp/c-language/type-float?view=msvc-170 - 범위
- https://boycoding.tistory.com/152 - 반올림 오류
- https://steemit.com/kr/@modolee/floating-point - 정밀도 오류
